(You can click the link to our Compound Interest Calculator page or read this guide)
The Ultimate Guide to Compound Interest Calculators: From Excel Formulas to Practical Dollar-Cost Averaging
Introduction:
From Spreadsheets to Trading Strategies: The Beginning of a Journey
Hello, friend! Welcome to this space.
I know that as you click into this article, several thoughts may be swirling in your mind.
Perhaps, like me years ago, you're staring at a blank Excel spreadsheet, feeling a bit lost. You've heard about the magic of compound interest and yearn to apply it to your savings or trading profits. Yet, faced with complex formulas and cells, you feel a bit lost, constantly asking yourself: "How exactly do I calculate compound interest in Excel?"
Or perhaps you're an active Forex trader where time is money. What you need isn't a slow spreadsheet build, but a Forex compound interest calculator that instantly tells you, "If I make 2% weekly, how much will my account be in six months?" You seek efficiency and precision.
Or perhaps you're just starting your financial journey, still grasping concepts like "simple interest" and "compound interest." You're looking for a clear explanation to help you take that first step toward planning your future.
Regardless of which scenario applies to you, I want to tell you: you've come to the right place. Seriously. This article isn't just a cold tutorial—it's more like a comprehensive sharing of my personal experience. I'll take you on a complete journey—from grasping the core concept of compound interest, to building complex dollar-cost averaging models in Excel with your own hands, to ultimately discovering and using a smarter, more convenient tool. I firmly believe that as investors and traders, we must not only know what but also understand the why. This article exists to achieve precisely that goal.
Core Concept Breakdown: The World of Difference Between Simple and Compound Interest
Before diving into any calculation methods, allow me to spend a few minutes discussing a seemingly basic yet crucial concept. Only when you truly grasp the "magic" of compound interest will your subsequent learning and calculations become meaningful.
Imagine this scenario: You have two friends, Xiaoming and Xiaohong, who each deposit 10,000 $ on the same day at an annual interest rate of 10%. The only difference is that Xiaoming chose simple interest, while Xiaohong opted for compound interest.
A's Simple Interest World: In the world of simple interest, interest is always calculated based solely on the original principal. So, every year, Xiaoming earns 10,000 $ * 10% = 1,000 $ in interest. This amount remains fixed, year after year. It's like a diligent employee receiving a fixed monthly salary—stable, but lacking the thrill of growth.
End of Year 1: 10,000 (Principal) + 1,000 (Interest) = 11,000 $
End of Year 2: 11,000 + 1,000 (interest) = 12,000 $
End of Year 5: Total interest earned: 5 * 1,000 = 5,000 $. Account balance: 15,000 $.
B's Compound Interest World: In Xiaohong's compound interest world, things get interesting. In the first year, she also earns 1,000 $ in interest, bringing her account total to 11,000 $. But starting from the second year, the magic happens: interest is no longer calculated based on 10,000 $, but on the new total of 11,000 $! This means her interest itself begins to "earn" interest.
End of Year 1: 10,000 * 10% = 1,000 interest, total 11,000.
End of Year 2: 11,000 * 10% = 1,100 interest, total 12,100. See? She earned 100 more than Xiaoming.
End of Year 5: Her account balance reaches 16,105.1 $, surpassing Xiaoming's by 1,105.1 $.
And this is only after 5 years! If extended to 30 years, A's account would be 40,000 $, while B's would reach a staggering 174,494 $! This is the power of compound interest—it's not a straight line, but a beautiful, accelerating exponential curve. Like a snowball rolling downhill, given a long enough slope (time) and sufficiently wet snow (return rate), it grows exponentially larger, eventually triggering an avalanche effect.
| Feature | Simple Interest | Compound Interest |
|---|---|---|
| Calculation Basis | Based solely on the initial principle | Based on principal + accumulated interest |
| Growth Pattern | Linear growth (like climbing stairs) | Exponential growth (like riding a rocket) |
| Wealth Effect | Steady but slow | Extremely powerful over the long term |
| Core Principle | Interest is "dead" | Interest is "alive" and self-replicating |
Understanding this captures the essence of long-term investing. Now, let's learn how to quantify this "magic."
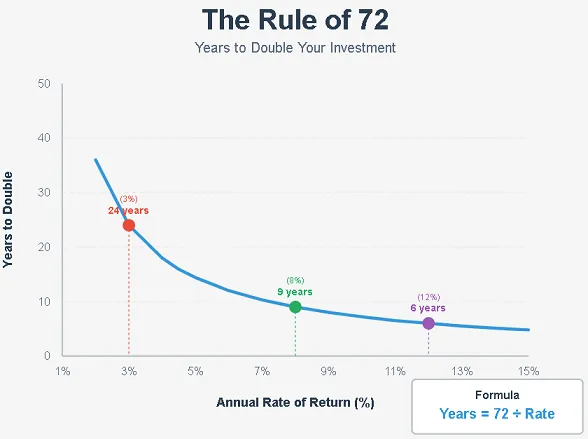
The Investor's Mental Math Secret: Quickly Estimate Your Wealth Growth with the Rule of 72
Before diving into complex Excel formulas, I want to share a personal favorite "secret weapon"—the Rule of 72. It's not just a math trick; it's more like a superpower that gives you rapid intuition about wealth growth in any situation. Whether chatting about investments with friends or evaluating a financial product, it delivers astonishingly accurate estimates in seconds.
The Rule of 72 is incredibly simple:
Divide 72 by your annualized return rate. The result approximates the number of years needed for your principal to double.
Formula: Doubling Period ≈ 72 / Annualized Return Rate (%)
Pretty straightforward, right? Let's explore a few examples to see its power:
Scenario 1: Bank Savings.Suppose you deposit money into a financial product yielding 3% annual interest. How many years would it take for your money to double? 72 / 3 = 24 years. Yes, you'd need to wait a full 24 years.
Scenario 2: Index Fund Investment If you invest in a stock index fund with a historical average annualized return of 8% (like the S&P 500's long-term average), how long will it take for your investment to double? 72 / 8 = 9 years. In just 9 years, your $100,000 becomes $200,000, and $200,000 becomes $400,000.
Scenario 3: An Ambitious Trading Goal As a trader, you set an annualized profit target of 20%. If achieved, your capital would double in: 72 / 20 = 3.6 years. This pace is astonishing—though it comes with extreme risk and difficulty.
Why is the Rule of 72 so important?
1. It gives you a "feel" for return rates: When someone tells you a product offers a 12% return, your brain instantly translates: "Oh, that means it doubles in 6 years (72/12=6)." This is far more intuitive than a dry percentage figure.
2. It helps you spot unrealistic promises: If someone pitches a project "guaranteed to double annually," that implies an annualized return rate of 72%! Your first reaction should be: This is highly likely a scam.
3. It reinforces long-term thinking: Through this rule, you clearly see that even seemingly modest returns (like 6%-8%) can generate immense wealth over time. It makes you cherish "time" as your most crucial investment partner.
Of course, we must clarify: the Rule of 72 is an estimate, most accurate within a 6% to 10% return range. Yet as a rapid mental calculation tool, its practical value is unmatched. In my view, this should be the first financial principle every investor masters.
Now that you've mastered this quick estimation "soft skill," let's dive into the "hardcore skill" of precise calculation.
The DIY Journey: How to Calculate Compound Interest Precisely in Excel
Alright, friends, now we're diving into the "hardcore" part. I know many people get overwhelmed just seeing Excel formulas, but trust me—I'll peel back the layers like an onion, revealing the secrets clearly step by step. Mastering this skill means you gain the ability to independently build and validate your own financial models, which is a powerful source of confidence.
Basics: Calculating Compound Interest for Lump Sum Investments
This is the simplest and most common scenario. Suppose you have an initial sum of money that you invest all at once, letting it grow quietly over the years.
Scenario: You have an initial investment of $10,000 USD. You find an investment opportunity with an annualized return rate of 8%, planning to invest for 10 years with compounding occurring once per year.
Steps:
1. Set up your worksheet: Open Excel and create the following tabs as shown below for clarity.
Cell A1: Present Value (PV)
Cell A2: Annual Interest Rate (Rate)
Cell A3: Number of Years Invested (Nper)
Cell A4: Payment Per Period (Pmt)
Cell A5: Future Value (FV)
2. Enter Your Data:
Cell B1: -10000 (Note! This must be negative. In Excel's financial functions, money leaving your pocket is represented by negative values—a crucial habit.)
Cell B2: 8% (or enter 0.08)
Cell B3: 10
Cell B4: 0 (since we're not considering additional future payments)
3. Work the magic—enter the FV formula: In cell B5, the exciting moment arrives! Enter this formula: =FV(B2, B3, B4, B1)

Press Enter, and Excel will instantly give you the answer: $21,589.25.
Formula Deep Dive FV(rate, nper, pmt, [pv], [type])
rate (interest rate): The interest rate per period. In our example, this is 8% from cell B2.
nper (number of periods): The total number of interest periods. In our example, this is 10 years from cell B3.
pmt (payment): The fixed amount paid each period. Here, it's 0 from cell B4.
[pv] (present value): Your initial principal amount. Here it's -10000 in cell B1.
[type] (payment timing): Specifies whether payments occur at the beginning or end of the period. We usually omit it, as the default is end-of-period.
See? Not too difficult, right? You've successfully put Excel to work for you. But the real challenge and value lies in the next step—when we start making regular additional investments.
Advanced: Complex Compound Interest Calculations with "Monthly Investments"
This is where most people get confused, and where your expertise truly shines. In the real world, most of us don't invest a lump sum all at once. Instead, we invest a portion of our income each month, much like saving.
My personal experience: Around 2015, I started trading and achieved some consistent profits. I was thrilled and wanted to know what my account would look like after one year or three years if I reinvested a portion of my monthly profits (say, $500) alongside my initial principal, assuming a certain monthly return rate. I opened Excel, expecting it to be straightforward, only to discover my FV formula knowledge was completely inadequate. I tried various complex manual calculations, ending up with messy spreadsheets and frequent data errors—it was incredibly frustrating. That experience made me determined to master it once and for all.
Now, I'm sharing the "ultimate formula" I developed back then.
Scenario: You have an initial principal of $10,000 and plan to invest a fixed $500 monthly on top of that. Assuming your investment offers a 12% annualized return, you want to know the total account balance after 5 years.
Key Point: All parameters must be standardized to a "monthly" dimension!
Monthly Rate (Rate): 12% annualized, so the monthly rate is 12% / 12 = 1%.
Total Periods (Nper): Investing for 5 years equals 5 * 12 = 60 months.
Monthly Payment (Pmt): -500 (Similarly, this represents money leaving your pocket, so use a negative value).
Present Value (PV): -10000 (also negative).
Steps:
Update your worksheet:
A1: Present Value (PV) -> B1: -10000
A2: Annual Interest Rate -> B2: 12%
A3: Investment Term -> B3: 5
A4: Monthly Investment (Pmt) -> B4: -500
A5: Future Value (FV)
Enter the "Ultimate Formula": In cell B5, enter this formula—it looks a bit long but has very clear logic: =FV(B2/12, B3*12, B4, B1)
Press Enter. The answer is: $59001.8.
Pretty mind-blowing, right? Over 5 years, your total investment is
10,000+(10,000+(500 * 60) = $40,000. Yet your account holds over $59001.8! That extra $19000+ is the miracle created by compound interest and consistent investing.
Formula Deep Dive: The essence lies in B2/12 and B3*12. This tells Excel we're shifting from annual to monthly frequency. We've converted the annual interest rate to a monthly rate and the number of years to months, perfectly aligning with our "monthly investment" behavior.
Mastering this formula puts you ahead of 90% of Excel users. Yet, you might also sense—as I did back then—that the process remains somewhat cumbersome. Especially when you need to quickly compare different scenarios (like investing $500 vs. $800 monthly, or 8% vs. 10% returns), repeatedly tweaking Excel spreadsheets and formulas isn't very efficient.
This is precisely why I created this website and developed these tools.
A Smarter Choice: Our Free Compound Interest Calculator Built for You
The Active Investor's Dilemma: Excel's Limitations
I hold Excel in high regard—it's an unparalleled tool. But as an active trader and investor, I know it's not the optimal solution in certain scenarios.
Time-consuming and error-prone: As we just demonstrated, you must meticulously set up cells, input correct formulas, and ensure no sign errors. In fast-paced trading markets, even minor operational mistakes can drastically skew your future projections.
Not suited for quick simulations: If you want to compare "Plan A: Invest for 5 years at 8% annualized, contributing $300 monthly" versus "Plan B: Invest for 7 years at 6% annualized, contributing $500 monthly," you'd need to repeatedly tweak multiple parameters in Excel. This process is cumbersome.
Mobile inconvenience: Inspiration and opportunities can strike anytime. When you're checking market trends on your phone or discussing an investment idea with friends, you can't conveniently open a complex Excel spreadsheet for calculations.
Distractions: Focus is paramount in trading. Your most valuable energy should be directed toward analyzing markets and managing risk, not battling Excel cells.
It was precisely because I experienced these pain points firsthand that I realized we needed a smarter solution.
Built for You: A Fast, Accurate, Focused Online Calculator
Discover one of our website's core tools—the Compound Interest Calculator. Crafted from my years of investment and trading experience, it's tailored for investors like you and me. Its design philosophy: Eliminate all unnecessary complexity so you get the results you need in seconds.
Why is it a better choice?
1. Ultimate Ease of Use: No need to memorize any formulas. Just a few clear input fields: initial principal, monthly investment, annualized interest rate, investment term, and compounding frequency. Enter your numbers, click "Calculate," and see the results instantly.
2. Built for Simulation: Adjust any parameter like playing a game and watch the results change in real-time. Curious how a 1% interest rate increase affects your outcome? Just tweak the number—you'll know in a second.
3. Complete Transparency & Security: I want to make this clear: All our calculators are pure front-end tools built with JavaScript. This means all calculations occur within your browser. No financial data is sent to our servers—we neither store nor can store any of your information. No registration, no login required. Completely free and absolutely secure. This trust is paramount to me.
4. Available anytime, anywhere: Whether you're using a computer, tablet, or phone, as long as you have a browser, it's ready and waiting.
Moving from cumbersome Excel formulas to this streamlined online tool isn't just an evolution of the tool itself—it's an evolution of our investment mindset. It frees us from the quagmire of "how to calculate," allowing us to focus more energy on the core question: "How to make better decisions?"
Beyond the Numbers: Real-World Factors You Can't Ignore
Friends, so far we've mastered the "technique" of calculating compound interest. But a true, seasoned investor must also possess the ‘insight' to understand reality. Those enticing figures we calculate are derived in a vacuum—an idealized laboratory. In the real world, two "invisible hands" quietly erode your gains. We must expose them.
The Inflation Trap: Calculating Your "True Rate of Return"
This is the most overlooked point by the vast majority of investors, especially beginners. When you see your investment account grow by 10% this year, you might be thrilled. But what if this year's inflation rate is 3%? That means prices for everything have risen by 3%, and the purchasing power of your money has decreased by 3%. Your 10% gain isn't a true gain.
1. Nominal Rate of Return: This is the unadjusted, surface-level return displayed on our calculator. In our example, it's 10%.
2. Real Rate of Return: This is the percentage by which your purchasing power actually increased after accounting for inflation. This is the number that truly matters to you.
A simple approximation formula helps us calculate it quickly:
Real Rate of Return ≈ Nominal Rate of Return - Inflation Rate. So, 10% - 3% = 7%. Your wealth's purchasing power has actually only grown by about 7%.
A more precise formula is:
Real Rate of Return = [(1 + Nominal Rate of Return) / (1 + Inflation Rate)] - 1 [(1 + 0.10) / (1 + 0.03)] - 1 = [1.1 / 1.03] - 1 ≈ 0.0679, or 6.79% Why does this matter? According to the U.S. Bureau of Labor Statistics, the U.S. Consumer Price Index (CPI) has risen by an average of about 2%-3% annually over the past few decades. If your chosen investment yields only a 2% annual return, your real return after inflation could be close to zero—or even negative! You're merely making money "on paper," while your purchasing power stagnates or declines.
So starting today, make it a habit: whenever you look at any investment return, mentally subtract the current inflation rate. This will give you a clearer, more realistic understanding of your investments.
Tax and Fee Reminder
Another "invisible hand" is taxes and various transaction fees. The future value calculated by our tool represents pre-tax income. In most countries, your investment gains—whether interest, dividends, or capital gains—are subject to taxation.
Capital Gains Tax: When you sell an appreciated asset, you pay tax on the value increase.
Interest/Dividend Tax: Interest and dividend income may also be taxable.
Transaction Fees: Brokerages or platforms may charge commissions when buying or selling investment products.
These factors further reduce your net returns. While our calculator omits these complex variables for simplicity, you must be aware of them. I am not a tax expert and cannot provide tax advice, but I strongly recommend consulting a professional tax advisor to understand your local tax laws before making significant investment decisions.
Important Guidelines and Compliance Statement
Friend, after sharing so much knowledge and tools, I must address the following points with the utmost seriousness and responsibility. This protects you and upholds our website's fundamental principles.
1. This is a tool, not investment advice (A Tool, Not Financial Advice): Please understand that all calculators provided on this site, including the compound interest calculator, are solely educational and informational tools based on mathematical models derived from your inputs. Their results do not constitute any form of financial, investment, tax, or legal advice. Each individual's financial situation and risk tolerance are unique. Before making any decisions that may impact your finances, consult a qualified, licensed professional.
2. Assumptions vs. Reality: The "annualized return rate" in the calculator is a hypothetical value. All investments, especially in high-risk markets like forex and stocks, involve uncertain returns, and past performance does not guarantee future results. You may experience losses, including the potential loss of your entire principal. Never treat the future value generated by the calculator as a promise or guarantee.
3. Garbage In, Garbage Out: The accuracy of our tool relies entirely on the accuracy of your input data. If you enter unrealistic return rates or incorrect principal amounts, you will only receive an unrealistic and inaccurate future projection. Please input each parameter rationally and objectively.
4. Limitations of the Simplified Model: For ease of use, our calculator employs a simplified model. It does not account for complex variables such as taxes, transaction fees, inflation, or irregular contributions mentioned in the previous section. Please treat the results as idealized, unadjusted reference values.
Conclusion: Embark on Your Compound Interest Journey
My Personal Perspective and Insights
Reaching this point, I find myself deeply moved. For me, compound interest has long transcended a mere financial concept. It embodies a worldview, a philosophy of life. While we've spent considerable time discussing the compounding of money today, the truth is that all the most beautiful things in life follow the principle of compound growth.
Your knowledge compounds through daily learning; Your health can compound through daily exercise and mindful eating; Your relationships can deepen through consistent, genuine effort and communication. Conversely, bad habits, procrastination, and neglect will also compound to erode your life.
My passion for trading and investing—and the reason I created this website—goes beyond financial returns. More importantly, it forces me to confront the law of compounding. It teaches me patience, for I know true growth takes time; it teaches me discipline, for I know every small, correct decision will amplify in the future; it teaches me reverence for the market, for I know risk also accumulates through compounding.
So when you use this little calculator, I hope you see more than just a number. I hope you see the powerful, universal law behind the number. Then apply it to every aspect of your life. Consider: Beyond money, what else in your life do you want to grow through compounding? This, perhaps, is the most valuable takeaway this article offers—beyond the calculations themselves.
Summary and Actionable Recommendations
Today, we've journeyed through a long yet fruitful path. We have:
1. Gained a deep understanding of the fundamental difference between simple and compound interest.
2. Learned to perform quick mental calculations using the Rule of 72.
3. Mastered the advanced skills of calculating basic compound interest and complex dollar-cost averaging in Excel.
4. Experience our convenient and secure online compound interest calculator.
5. Recognized the impact of real-world factors like inflation and taxes on investment returns.
Now, it's time to turn knowledge into action:
Action 1: Open our Compound Interest Calculator immediately. Enter your own financial goals and "play around" with it yourself to feel the huge differences different parameters can make.
Action 2: Create a small, actionable dollar-cost averaging plan for yourself. Even if it's just $100 per month, starting is the most crucial step.
Action 3: Keep the concept of "real return rate" firmly in mind. When evaluating any future investment opportunity, always ask: "How much remains after inflation?"
Final Risk Warning
Investing involves risks; proceed with caution. Financial markets are highly volatile, and no strategy or tool guarantees profits. Invest only within your risk tolerance and take full responsibility for your financial decisions.
Further Reading
After mastering long-term growth planning, understanding how to manage risk and calculate returns in each specific trade is equally crucial. I highly recommend exploring these complementary in-depth articles on our website:
The article on the Position Size Calculator : Teaches you to scientifically calculate how much capital to allocate per trade based on your risk tolerance.
The article on the Risk/Reward Calculator : Helps you clearly assess a trade's potential profit and loss before opening a position, enabling smarter decisions.
The article on the Pip Value Calculator : Essential reading for forex traders, as this forms the foundation for calculating profits and losses.
Thank you for your patience in reading this. I hope my insights illuminate your path forward. On the journey of compound growth, let us grow together.

Leave a Comment: