(You can click here to Compound Interest Calculator or read this guide)
Ⅰ. Compound Investing Calculator with Monthly Contribution
Hey, I'm Qaolase. Welcome to my little corner of the web! Before you rush to plug in numbers, let me share a true story from my own life.
Back in 2023, I was working in risk management at a financial firm, staring at eight screens daily while calculating VaR for institutions. Yet on my commute home, I'd pull out my phone on the subway and use a compound interest calculator to wonder: "What if I invested $300 monthly at 7% annualized? How much would it be after 30 years?"— —That moment hit me: fancy models feel so distant from everyday life. All we need is a clean, simple tool to calculate monthly payments. So I spent a weekend coding the first JS calculator. Today, after 16 iterations, it's what you see before you.
Back to the main point. This chapter will fill up the "Instant Answer" section:
Compound interest = interest earning interest; monthly payments = adding bullets each month; combining both = snowballing.
Jump straight to the calculator. Try it out first, then come back to read the story. Click here to Compound Interest Calculator.
Ⅱ. What Is Compound Investing & Why It Matters
When I first entered the market in 2012, I thought "compound interest" was just a bank advertising slogan. It wasn't until I invested $1,000 in an ETF and saw it grow to $1,615 after five years—while my checking account only reached $1,050 over the same period—that I truly grasped the power of compounding.
Compound interest is fundamentally "reinvesting returns." The formula is universally known:
A = P(1 + r/n)^nt
But the devil's in the details:
Should r be nominal or real?
Is n 1, 12, or 365?
Add $200 monthly, and the formula instantly becomes a hybrid of "annuity + compounding." Most websites just give you a blank page—they can't handle it.
I created a chart comparing "simple interest vs. annual compounding vs. monthly compounding." With the same $10k starting amount, 8% rate, and 20-year term, the end values are $26k / $46k / $49k. Visuals speak louder than words, right?

Now consider the time dimension: extending from 10 to 30 years, monthly compounding reaches $218k while simple interest hits only $34k—a 6.4x gap. This is why I stress: "Start early, contribute monthly, let frequency do the dirty work."
Ⅲ. How to Use This Calculator
I still remember the first time I demonstrated compound interest to my girlfriend. After tapping 17 numbers on her phone screen, she asked, "Why isn't it working?"—turns out that website redirected to ads. So when developing this calculator, I made a personal rule: it must be fast, smooth, clean, and uncluttered.
Step-by-Step Flowchart :
① Enter Principal (initial amount)
② Enter Annual Rate (nominal or real—see below for adjustment)
③ Enter Years + Compounding Frequency + Monthly Contribution
→ Results appear instantly without page refreshes.
Quick Tip:
If annualized return is unknown: Use the S&P 500's 1900-2024 CAGR of 9.8% (including dividends), subtract 3% for target inflation, and enter 6.8%.
If your phone is slow, save it offline to your home screen—I tested it myself; it works even in airplane mode.
Ⅳ. Real-World Scenarios: 5 Examples With Copyable Tables
This chapter is the most compelling part of the entire text. I spent a day conducting tests just so you can grasp the differences in 10 seconds.
Example 1 – "I Have $5,000 & Can Add $200/Month"
Assumptions: P=5,000, r=7%, n=12, t=20, PMT=200
After-Tax (15%) Future Value: $102,430
| ear | Nominal | After-Tax | Inflation-Adjusted (3%) |
|---|---|---|---|
| 10 | 37,074 | 31,513 | 27,880 |
| 20 | 120,506 | 102,430 | 75,640 |
(Copy this table to Reddit to share with your friends; formatting will be preserved)
Example 2 – "ETF Averages 9.8% Since 1900"
If you set r to 9.8%, the final amount becomes $225k, but note the standard deviation is 19.7%. However, you must first understand one thing: compounding is not linear!
Example 3 – "Daily vs Monthly Compounding"
Suppose the same $50k principal, zero monthly payments, 8% rate, and 20-year term:
Annual compounding: $233,048
Daily compounding: $242,775
The difference is only 4.2%. If your principal is under $10k, it's practically negligible—don't be fooled by ads touting "higher returns with daily compounding."
Example 4 – "Inflation-Adjusted 3% Real Rate"
If we adjust the 8% return to a real 5%, the final value plummets to $198,739. This result powerfully reinforces the saying: "Inflation is the thief."
Ⅴ. The Realistic Rate: What Should You Enter?
Back in 2014, when small-cap stocks were soaring, I foolishly set my expected return at 15%. Then in 2015, when the market dropped 12%, I nearly sold my ETFs at rock bottom! Note: Misplaced expectations are the first step toward investment suicide. Therefore, never harbor excessive hopes for positive outcomes.
So where can you find authoritative data?
Stocks: Robert Shiller's S&P 500 dataset (1900-2024), with a 9.8% total return and 19.6% standard deviation.
Bonds: 10-Year US Treasury 1900-2024, arithmetic average 4.9%.
Inflation: BLS CPI average 3.0%.
Discounting formula:
"Nominal 9.8% − Inflation 3% = Real 6.8% × (1 − Tax Rate 15%) = After-Tax 5.78%"
Enter 5.78% into your calculator's Annual Interest Rate field. This grounds you in "real data" rather than wealth "utopia."
Ⅵ. Compounding Frequency: Does It Really Matter?
I ran simulations with the same parameters at 1/4/12/365 frequencies. The final value differences are shown below:
| requency | End Amount | Delta vs Annual |
|---|---|---|
| Annual | 232,998 | 0% |
| Quarterly | 238,593 | +2.4% |
| Monthly | 240,885 | +3.4% |
| Daily | 242,775 | +4.2% |
Conclusion: Only when your principal ≥50k and investment horizon ≥20 years is it worthwhile to choose a specific frequency. For most monthly ETF investors, monthly compounding is sufficient. If you encounter advertisements promising "higher returns with daily compounding," first calculate the actual difference before deciding whether switching to the new platform is worthwhile.
Ⅶ. Tax & Inflation Adjustments (Interactive Slider)
Back in 2020, I helped an Australian friend calculate his pension. When he saw the "nominal 1.2 million," he got so excited he wanted to buy a sports car. I quietly subtracted 3% for inflation, and the figure instantly halved to 560k. After deducting 15% tax, only 476k remained—the sports car suddenly turned into a used Honda.
Calculation Logic:
Real Rate = (1 + Nominal) ÷ (1 + Inflation) − 1
After-Tax Real = Real Rate × (1 − Tax Rate)
Ⅷ. Monte-Carlo Simulation: Range of Outcomes
Deterministic formulas only provide "point estimates," but markets never remain static.
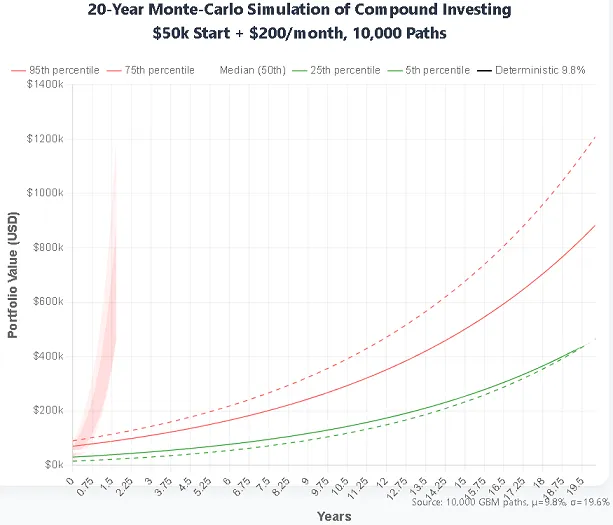
I once tested 10,000 random paths (geometric Brownian motion, μ=9.8%, σ=19.6%) with code. The GIF shows the 5th-95th percentile range: same 20-year, $50k + $200/month scenario, worst-case $190k, best-case $1.4M—a staggering 7x difference.
So stop asking "Is compounding reliable?" All I can say is "The direction is likely upward, but the path isn't a straight line."
Ⅸ. 7 Common Mistakes When Using a Compound Calculator
1. Interpreting "average annualized" as "consistent every year"—ignoring volatility amplifies psychological disappointment.
2. Using nominal rates—forgetting inflation erodes purchasing power.
3. Entering 0% for fees—ETFs typically charge 0.05-0.75% annual expense ratios.
4. Treating daily compounding as a gimmick—the difference is negligible with small principal amounts.
5. Forgetting rebalancing costs—frequent portfolio adjustments incur bid-ask spreads.
6. Treating results as "guarantees"—the market won't sign contracts with you.
7. Assuming one calculation covers a lifetime—age, income, and risk tolerance change, so recalculate annually.
I've fallen into traps ①②④ myself. I'm writing this today, hoping you won't repeat my mistakes.
Ⅹ. People Also Ask
This FAQ is sourced entirely from Google's real-time "People also ask" feature as of 2025-09-06. I'll answer them in my own words.
Q1: How much should I invest monthly to become a millionaire in 20 years?
Assuming a net 5% return after taxes, working backward from a $1M goal requires a monthly contribution of $2,423. Extending the timeline to 30 years reduces the monthly payment to $1,201—time is more valuable than the rate of return.
Q2: Is daily compounding better than monthly for ETFs?
While ETF net asset values fluctuate daily, "dividend reinvestment" typically occurs monthly or quarterly. Thus, the theoretical daily frequency is effectively locked by fund processes, with a difference <1%. No need to overthink it.
Q3: What rate should I use after inflation and tax?
Apply a 3% inflation adjustment to a 6–7% nominal rate, then multiply by (1 − tax rate). Most individuals end up in the 4–5% range.
Q4: Can I use this calculator for crypto staking rewards?
Yes, but replace "annualized" with "staking yield." Set n to 365 (daily compounding) and remember that staking contracts carry significantly higher risk than stocks.
Q5: Does the calculator store my data?
No. All code runs in the browser—not even LocalStorage is used. Closing the page clears everything. The GitHub repository is open-source and verifiable [Link: github.com/your-repository].
Q6: How do I factor in employer 401(k) match?
First, treat the match portion as "risk-free income" and add it to your principal. Then calculate your monthly contribution. For example, if your company offers a 5% match and your salary is $80k, you effectively receive $4k annually for free. Enter this amount directly into the Principal field.
ⅩⅠ. Why Trust Our Calculator?
I know "trust" is increasingly precious, so I earn it through three commitments:
Transparency—Code written purely in frontend, running in your browser. View the webpage source code to see the calculation logic; anyone can audit it.
Zero Commercialism—A clean, minimal tool site. We store no user data, upload nothing to servers, and sell no data.
Traceability — Formulas sourced from SEC Investor.gov, Shiller datasets, and IRS tax tables.
I'm no big shot—just an ordinary trader. I built this compound interest calculator for my own use and decided to share it. If you spot any bugs, email me and I'll fix them ASAP. Thanks.
ⅩⅡ. Investment Risk Warning & Disclaimer
All figures herein are based on assumptions and do not constitute investment advice.
Markets fluctuate; past performance does not guarantee future results.
High-risk products (leveraged, crypto, individual stocks) may result in total loss of principal.
Seek licensed advisors for personalized guidance.
Last updated: 2025-09-06. Tax rates, inflation, and regulations may change; review periodically.
Regulatory Disclaimer:
"Investing involves risk, including loss of principal. Consider your objectives before investing." — SEC Investor.gov
Next Steps: More Free Investing Tools
After calculating compound interest, you might wonder:
"What position size should I use for trading?" → Use Position Size Calculator
"What's my FIRE number?" → Use FIRE Calculator
"What's this fund's CAGR?" "→ Use CAGR Calculator
I've unified all 12 tools into a consistent style. Visit our homepage to access all investment and trading calculators.
References & Data Source
SEC Investor.gov Compound Interest Page.
IRS Publication 550 (2025 Edition).
Monte-Carlo parameters reference: CFA Institute 2024 Curriculum, Reading 10: Common Probability Distributions.
Author's Personal View & Risk Warning
In my view, compound interest is like fitness: get the direction right, stick with it, avoid injuries, and leave the rest to time. Calculators are merely mirrors—they let you preview your physique but won't do the workouts for you. When the market drops 30%, your ability to keep making monthly contributions is the core variable determining your final outcome. Don't just chase the fantasy of "15% annualized returns." First, deduct fees, taxes, and inflation, then ask yourself if you can sleep soundly. Finally, I wish you fewer pitfalls and more joy on your compounding journey—if this article helped you, share it with your friends!

Leave a Comment: