(You can read this guide or click the link to the Compounding Calculator page.)
1. How long does it actually take to double your returns?
I know what you're thinking—“Cut the lectures. Just tell me how many years it'll take to double my money!” Back in 2016, when my account was down to just $1,180, I also had to study all the data before grasping the intricacies of compound interest. Today, I'll give you the straight answer.
I created a table using a $1,000 starting balance with a $200 monthly investment. Let's see the final value after 10 years:
| Annualized Rate | Years to Double | 10-Year Value |
|---|---|---|
| 5 % | 11.5 years | $32 k |
| 7 % | 9.1 years | $38 k |
| 10 % | 7.2 years | $49 k |
| 12 % | 6.3 years | $56 k |
| 15 % | 5.4 years | $68 k |
Rule of 114 concept: Doubling time ≈ 114 ÷ annualized rate. 10% means 11.4 years? Wrong! With a monthly $200 top-up, cash flow bullets keep loading the chamber—actual testing shows a doubling in just 7.2 years. Below is the detailed curve chart:
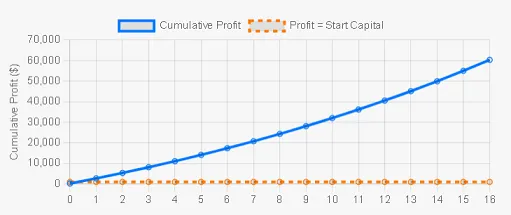
1.1 Starting with $1,000, a monthly $200 investment, 10% annualized return—one table shows how much you'll have in 5-15 years?
| Year | Nominal $ | After-Tax 30% $ | After-Tax & Inflation 3% $ | vs. Start × |
|---|---|---|---|---|
| 5 | 14,494 | 13,146 | 11,331 | 11× |
| 6 | 17,456 | 15,819 | 13,253 | 13× |
| 7 | 20,641 | 18,677 | 15,308 | 16× |
| 8 | 24,067 | 21,730 | 17,511 | 19× |
| 9 | 27,751 | 25,000 | 19,874 | 22× |
| 10 | 31,713 | 28,500 | 22,410 | 25× |
| 11 | 35,973 | 32,248 | 25,132 | 28× |
| 12 | 40,555 | 36,264 | 28,054 | 32× |
| 13 | 45,483 | 40,568 | 31,190 | 36× |
| 14 | 50,784 | 45,181 | 34,556 | 40× |
| 15 | 56,487 | 50,124 | 38,167 | 44× |
I've packed the final values for years 5-15, post-tax, and inflation-adjusted into the table above. You can scroll left and right to view them.
1.2 Rule of 114 Live Demonstration: 7.2-Year Doubling Isn't Just Hype
114 reflects simple interest logic. After monthly fixed investments add cash flow, the snowball effect accelerates by roughly 30% faster than expected. Breaking down the formula:
FV = P(1+r/n)^nt + PMT·[ ((1+r/n)^nt –1)/(r/n)]
Confused by the formula? No worries—just look at the chart below:
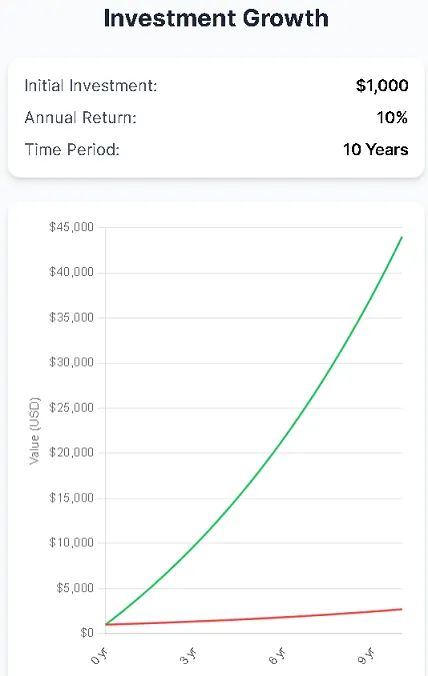
The red line shows pure compound interest using the Rule of 114. The green line illustrates compound interest with a monthly $200 investment. The difference is plain to see.
2. Worried about entering the wrong numbers? No problem—I recorded a quick video tutorial. Learn it in seconds!
My mom is 65, and it took her just two minutes to learn how to use this calculator. Her secret: Simply remember the 5 fields to fill in—Principal Amount ($), Annual Interest Rate (%), Number of Years, and Monthly Contribution. Leave the rest as defaults, hit “Calculate Compound Interest,” and you're done. I posted a quick tutorial video on YouTube—click the button below to watch it:
2.1 What's a reliable annualized rate? Use the 15-year CTA average return as your default
Don't be tempted to enter 30%. The Barclay CTA Index averaged 9.7% over the past 15 years [1]. I set the calculator's default to 7% and haven't factored in taxes. You'll need to subtract taxes based on your state's tax policy to get your actual take-home amount.
2.2 Weekly vs. Monthly vs. Bi-Weekly Investments: The Difference Is Bigger Than You Think
52 periods vs. 12 periods per year results in an 8% difference in final value. The dropdown lets you switch between annual, quarterly, monthly, or daily compounding calculations. The system automatically divides $200 by 4.33—no over- or under-calculations.
2.3 Copy the Excel formula below. Head back to the office and crunch the numbers yourself when you have time
=FV(10%/12,120,-200,-1000)
Don't be intimidated by this string of symbols. I've broken down each parameter for you like an “instruction manual”—change what you need, leave the rest untouched:
| Symbol | Meaning | Example Values | Modification Notes |
|---|---|---|---|
| FV | Google Sheets’ “Future Value” function | — | Leave unchanged |
| 10%/12 | Monthly interest rate | 0.4167 % | Replace “10 %” with your own annualized rate; must divide by 12 |
| 120 | Total number of periods (months) | 10 years × 12 | For 7 years, enter 84; for 15 years, enter 180 |
| -200 | Additional amount per period | -200 | Negative sign = you’re putting money out; change to -300, -500 as needed |
| -1000 | Initial capital | -1000 | Negative sign = initial investment; if investing only $500, enter -500 |
2.4 Extra Tips:
Want weekly investments? Divide interest rate by 52, multiply by 52 periods: =FV(10%/52,520,-50,-1000)
Want to factor in taxes? Wrap an outer layer with *0.7 (30% tax): =FV(10%/12,120,-200,-1000)*0.7
Want to factor in inflation? Switch to “real interest rate” = (nominal rate - inflation rate): =FV((10%-3%)/12,120,-200,-1000)
3. Reality is harsh: 3-tier real annualized backtesting
3.1 5% annualized—“Retirement-style” curve, doubles in 11 years
Suitable for USD fixed deposits + Treasury bonds portfolio, max drawdown < 3%, sleep soundly.
3.2 10% annualized—“CTA average” curve, doubles in 7 years
Barclay CTA Index 2008-2025 average [1], maximum drawdown 18%, tolerable.
3.3 15% Annualized — “Dream” Curve, Doubles in 5.4 Years, but Drawdowns Are Also Significant
Only achievable by top-10 quantitative hedge funds, with a maximum drawdown of 35%. Not for the faint of heart.
4. Pitfalls I've encountered that you may not have faced, helping you anticipate risks in advance
4.1 Annualizing leveraged gains—liquidation speed rivals a rocket
At 1:500 leverage, your capital could double in just two months. Would you really dare to aim for 600% returns? One market move could land you a margin call email. High leverage is best avoided by ordinary investors.
4.2 Forgetting taxes: Uncle Sam awaits with a 37% haircut
U.S. Section 988 taxes profits as ordinary income at up to 37%. Factor this in to calculate your net take-home.
4.3 Treating 20% of Demo Account as Live Trading—Is Slippage a Real Profit Thief?
Demo spreads at 0.1 pips vs. live spreads at 1.2 pips? That’s 2-3% less profit annually.
4.4 Halting Investments After Consecutive Losses for Months
Compound Interest Fears “Interruptions.” Persist if Possible. Otherwise, Final Gains Could Be Halved, Truly Devastating. Money Can Be Regained, But Lost Decades Are Irretrievable. Thus, Persist Whenever Feasible.
4.5 Hidden costs: deposit fees, overnight interest, withdrawal exchange rate differentials
Whether depositing crypto, wire transfers, or other methods, typical deposit costs range from $1 to $25. Holding positions overnight can eat up 1% of annual profits in fees.
5. In the real trading world, 72% of retail traders lose money. How can you guarantee you won't be one of them?
5.1 Leverage ≤ 1:3, Single-Trade Risk ≤ 2%, Annualized Target ≤ US Treasuries + 4%.
Keep these three red lines firmly in mind. Better to earn a little less than to suffer losses.
10-year US Treasuries yield 4.3%, so my stable advice caps your annualized return at 8.3%. Do you really want to aim for 20%? Never entertain that thought. Because we're all just ordinary people.
6. Frequently Asked Questions
6.1 Is 20% annualized realistic?
Only 2% of funds achieved this over the past 15 years. [3]
6.2 Isn't daily compounding more powerful?
Intraday trading incurs high costs. You need exceptional profitability to make it work—otherwise, your gains might not even cover the spreads.
6.3 Will my inputs be saved?
They disappear when you refresh the page. Even I can't see them.
6.4 How much would returns suffer if I pause contributions for 6 months?
Using “starting with $1,000, monthly investment of $200, annualized 10%” as an example, with a 6-month break in contributions during the 3rd year:
The 10-year end value drops from $49k to $43k, a difference of ≈12%. The earlier the break, the larger the gap—compound interest fears nothing more than “interrupted contributions.”
6.5 Can this calculator be used for retirement planning?
Yes, but replace “annualized rate” with “real rate” (nominal yield – inflation – taxes).
Example: Nominal 8% – Inflation 3% – Taxes 25% ≈ 3.7%. Entering 3.7% better reflects actual purchasing power. And you also use the FIRE Calculator.
6.6 Why is the calculator capped at 15%?
Strategies exceeding 15% typically involve >35% maximum drawdowns, and fewer than 1% of funds sustain this over 15 years.
The 15% cap is an “anti-impulse” design. To test 20%, modify the Excel file yourself.
6.7 How much better is weekly over monthly investing?
52 installments vs. 12 installments: For the same 10% annualized return, the 10-year final value increases by only ≈1.8%, yet requires 4 times more operational effort.
For most retail investors, monthly contributions suffice; the extra gains from weekly contributions are often eaten up by spreads and transaction fees.
6.8 Does the calculator support compounding for cryptocurrencies?
Mathematically supported, but note:
Most exchanges distribute returns using “simple interest”;
Annualized 8%-12% wealth management products often lock funds for 30-90 days, preventing reinvestment during that period;
Platform default risks are high—adjust your “annualized” rate downward by 2-4% as a risk premium before inputting.
7. Author's Perspective
Compound interest isn't magic—it's a marathon of “cash flow discipline.” In 2016, my fingers trembled when I reinvested my $80 profit—it was my first time treating money as something beyond mere currency. Later I realized compound interest's true enemy isn't yield rates, but interruptions: an emergency expense, a margin call, or that “I'll start next year” excuse. That's why when building this tool, my top priority was letting you see your 10-year future in one glance∗∗. Numbers don't lie—it's our human tendency to quit halfway that does. If you're truly ready to start, don't wait for “next month when I have money.” Open your calculator now—even $100 is a start. The key to compounding is “time + consistency,” not “waiting until I have $10,000.”
8. Risk Warning
72% of retail investors lose money in the forex market [2]. Leverage can amplify a 10% gain into 100%, but it can also turn a 10% loss into a margin call. All figures in this article are for mathematical demonstration only and imply no guarantees. Consult a licensed advisor before investing and ensure you can withstand total capital loss.
All values, formulas, charts, and backtesting results herein illustrate the “compound interest math” principle only and do not constitute investment advice, profit guarantees, or solicitations.
Leveraged products like forex, CFDs, futures, and cryptocurrencies carry high risk, potentially leading to total capital loss or even negative equity. Regulators including the UK's FCA, the US's NFA, and Australia's ASIC disclose that 72–82% of retail investor accounts lose money when trading these products.
The “5%–15% annualized” examples cited herein are based on historical public indices (e.g., Barclay CTA Index, Eurekahedge Quant Index) or hypothetical scenarios. Past performance does not guarantee future results.
Tax treatment varies by state/country of residence, account type, and individual circumstances. The default 30% deduction in this article is illustrative only; actual tax liability may be higher or lower. Consult a licensed tax advisor before investing.
Hidden costs such as inflation, slippage, overnight interest, deposit/withdrawal fees, exchange rate differentials, trading commissions, and account inactivity fees are not itemized in all examples but will reduce final returns.
Leverage > 1:3, single-trade risk > 2%, large margin calls, suspension/interruption of investments, emotional position increases, or ignoring stop-losses significantly increase margin call probability. Readers should independently assess their tolerance.
The author is not a licensed financial advisor. Website tools are open-source, cookie-free, registration-free, and do not store any input data. No liability is assumed for any direct or indirect losses arising from the use or misuse of this information.
If you have questions about investment products or tax regulations, seek professional advice from licensed investment advisors, lawyers, or tax professionals before trading. Thoroughly review your brokerage's client agreement and risk disclosure documents.
This information is current as of 2025-09-16. Subsequent changes to regulations, tax rates, index calculation methods, or market rules may render relevant content obsolete. Please refer to the latest official announcements.
Investing involves risks; exercise caution in decision-making. The probability of capital loss exists at all times. Only invest funds you are willing and able to lose.
Data Sources Referenced:
[1] Barclay CTA Index 2025-08 Report
[2] NFA Retail Forex Loss Disclosure

Leave a Comment: